图的最短路径算法
缘起
以前江苏高速收费是按照如下方法:根据车辆的入、出口站A和B,直接读取预置的从A站入路网从B站出路网的记录对应的金额。未来的发展方向是“自由流”收费,大致图景如下:弱化收费站的概念,取而代之在高速公路沿途设置一个个途径点,车辆每经过一处,行驶轨迹上就会再往前延伸至当前途径点,最终这些一个个彼此相邻的途径点形成了此次在高速路网中行驶的路线,以此作为收费的依据。
这就带来了一个问题。由于一些人为的或者客观的原因,车辆经过某(几)处途径点时,标识信息没有被记录,导致最终的行驶路线上出现了一些不相邻的途径点。这时,需要以最短路径的原则,恢复不相邻的点之间的那些点。这就回到了图论中经典的求给定图中任意两点间最短路径问题。
下面是我自己实现的算法。与已有的最短路径算法相比,可能与Dijkstra算法的思路更为接近。数据结构上,使用Java非静态内部类机制和HashSet,来存储任意节点的相邻节点和边;用previous指针(Java中更严谨的说法是引用)存储最短路径上的前一个节点。算法上,从任一节点为出发节点,以广度优先的原则向外扩散,不断调整其他各个节点到出发节点的最短路径。
示例输入
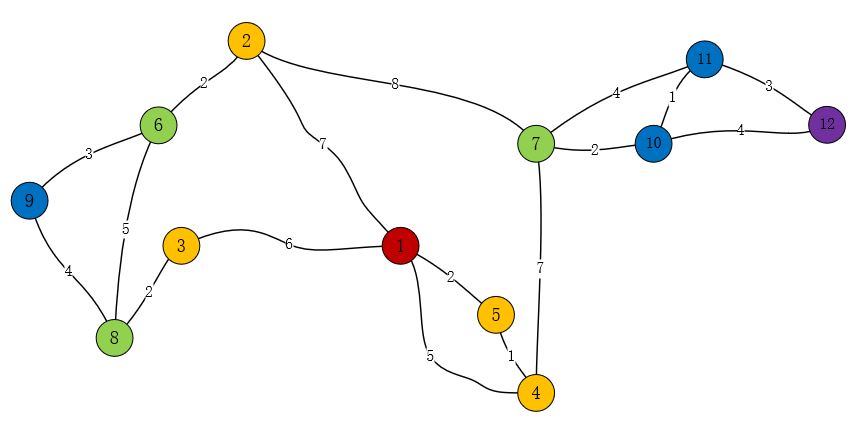
1号为此次的出发节点,相同颜色的若干节点到出发节点的“远近程度”相同。
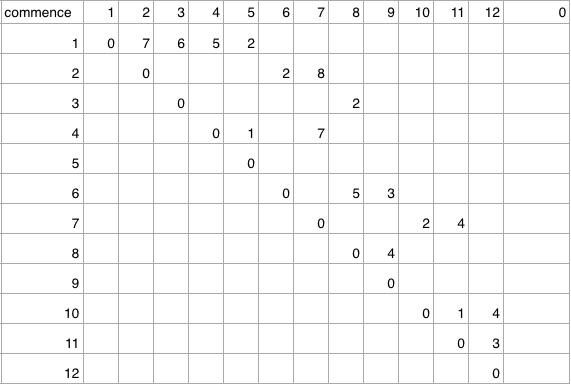
用邻接矩阵存储图,被程序读取以初始化(最右边一列的0用作读取文件时的终止标志)。
算法步骤
名词解释:
若图graph含有连通的A、B两点,则图中的有向边有两条,它们互为反向有向边;有向边的起点称为from,终点称为to,边的长度称为d。算法描述中,set表示有向边集合,queue表示有向边队列。每个节点存储一个shortest值(代表从开始节点到本节点的最短距离),和一个previous指针(表示从开始节点到本节点的有向路径上,本节点的前一个节点)。
- 给定graph和起始节点s,每个点的shortest均置为0
- 将以s为to的有向边放入set
- 将以s为from的有向边放入queue的尾部
- (main loop)从queue头部取出一条有向边e,若e不为null,执行5,否则结束循环
- 计算
e.d+e.from.shortest的值v,若e.to.shortest为0或大于v,则将e.to.shortest置为v,将e.to.previous指向e.from(每次改变previous指针的指向时,执行6),否则do nothing。然后,对于每一条“以e.to为from的有向边”(e的反向有向边除外,即不走回头路),均做如下操作:将其放入set,若放入成功,将其再放入queue的尾部,否则(此有向边之前已经计算过,不再计算第二遍)do nothing。继续执行4 - 遍历当前节点c的各个邻居节点n,若n的previous为c,则将n的shortest值置为
v=c.shortest+c与n间的距离。然后对n递归进行本步骤
结束循环时,graph中的任何一个节点,只要与s连通,都能沿着previous指针回溯到s。
注:在双向队列queue的尾部放入,头部取出,保证了以s往外的发散按照广度优先遍历进行。
程序源码
在此路径的src/main/java/daoning/graph/文件夹下